Lagrange Points
& why are they so important.

Lagrange points are gravitational equilibrium points. At such points, the forces exerted on any particular object are equal and cancel each other out. Consequently, that object stays in a stable position.
Lagrange points got their name from Joseph-Louise Lagrange, an Italian astronomer who discovered these equilibrium points in 1772. These points essentially allow any small object, like a spacecraft, to orbit at a fixed distance from the large bodies nearby.
The Earth and Sun system also have these points, in total there are five: L1, L2…, L5.
Before we dive into the discussion about them though, you need to know what Kepler’s third law of planetary motion is.
Where T is the time period of one orbit, r is the radial distance from the large body, G is the gravitational constant, and M is the mass of the larger body. In this case, M will be the mass of the Sun.
This law can be boiled down to a simple relation that follows:
Where p is the period, r is the radius, and c can be called the gravitational constraint. Why? Well, the cool thing is that the period at all these points remains the same, the radius is obviously changing so c must change accordingly.
L1
L1 point lies between the Earth and the Sun, it experiences major gravitational pull from the Sun and relatively less from the Earth. L1 point’s period is approximately equal to 1 Earth-year, even though its distance is shorter to Sun. This occurs due to Earth’s pull in the other direction.
L2
On the other hand, L2 lies right behind Earth. It is the exact opposite case of L1, and now its distance from the larger body – the Sun – is larger. But Earth’s gravity affects it in such a manner that its period remains unchanged from 1 Earth-year.
L3
L3 lies on the orbital path of Earth. Exactly 180 degrees to Earth. This point lies directly behind the Sun at all times. The Sun and Earth pull it in the same direction, and it experiences gravity in the direction of the Sun.
L4 & L5
L4 and L5 are mirror images of each other. They are the most stable Lagrange points, and they also lie on either side of the Earth on its orbital path. The distance from the L4/L5 to the center of Earth, and to the center of the Sun is the same. It sits at a point of this equilateral triangle, and the net gravitational attraction of this point is towards the †barycenter of the Sun-Earth system.
†Barycenter is the center of mass in which two bodies orbit. However, when one of those bodies is too large then the barycenter lies inside that body – which is also the case with the Sun-Earth system.
The most stable points are L4 and L5, and they have an oscillating trajectory that is tied to the Earth-Sun system’s motion. L1, L2, and L3, on the other hand, are much like saddle points. A little deviance in these points can result in an object at this point to continue falling in that particular direction.
L3 is not feasible because Sun is in-between and it can disrupt connections from the ground; secondly, a lot of orbit correction thrusts will be required periodically…dramatically raising the cost of keeping a satellite or a probe there.
These points (other than L3) are extremely important in deep space observation and space missions. They reduce fuel costs and provide almost stationary observation points which are important for satellites like JWST (it is quite close to L2, will cover it another time).


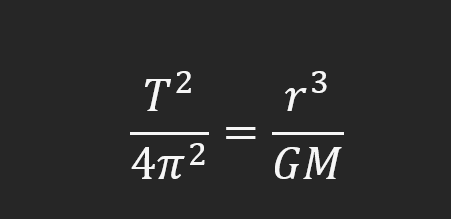


I also write about space and physics, if you can just check out. I know physics but I don't go deep while writing.